Handout #17 - Properties of Magnets

 

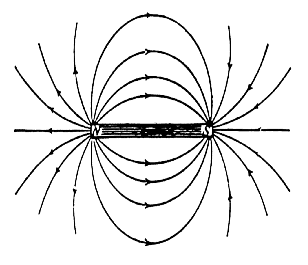The direction of the field at any point is defined as the direction of the force that would exist on the North pole of a magnet if it were placed in the magnetic field.  This is purely convention – we could also have used a South pole; we get exactly the same information about the nature of the field in both cases.  The direction is shown visually by arrows - these point away from N pole towards S pole according to our definition above.  Unlike fields from electric charges, the magnetic field is always self-connected.  In the drawings below, no line ever begins or ends, but rather always makes a complete loop.  This is a purely experimental observation, with one interesting consequence: no object exists which has only a North pole or only a South pole – every magnetic object necessarily has BOTH simultaneously, and the representation always includes fully closed magnetic field lines going from N to S and traveling through the inside of the medium.

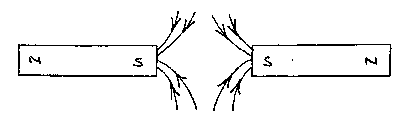
Right is a picture of the magnetic field of two magnets with like poles facing.


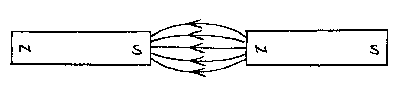
Left is a picture of the magnetic field of two magnets with unlike poles facing.

 

A magnet’s greatest strength is found at its poles, and its strength diminishes rapidly moving away from the poles. At a point about midway between its two opposite poles, a bar  magnet exhibits no magnetism at all, because the effects of the opposite poles cancel one another. The poles of a magnet are not necessarily of equal strength.

 

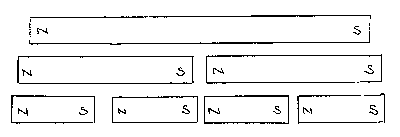
Left: Continuing this process of splitting indefinitely will only give you smaller and smaller complete magnets.

 

 If a magnetic piece of steel rod is cut into smaller pieces, each piece is a magnet with a N and a S pole – a complete (but smaller) magnet.  No matter how small of a piece we end up with from our original magnet, we always have a complete magnet with N and S poles.  This suggests one possible way of thinking about this phenomenon: every part of a magnet could be said to consist of lots of really tiny magnetic areas - all of which are lined up with their N poles pointing in the same direction. At the very tip ends, the magnetic field lines from the “free” end of the magnet. The poles of the tiny magnets repel each other and so the magnetic field lines fan out and eventually connect with the opposite “free” pole on the other side of the magnet.  This is what helps create the characteristic doughnut (torus) shape of the magnetic field.

Why is it that some objects are attracted to magnets and others seem totally indifferent to magnetic fields?  We cannot know if an object is magnetic unless we somehow test that fact – the only way we can test that fact is to use another magnet to see if it is repelled (why not attracted as well?).  If it is, we can claim that the first object is magnetized.  Using a non-magnetic material (like a piece of paper) for this test would be silly, since the paper would not ‘feel’ the magnetic field and would therefore not respond by attracting or repelling.  In other words, only objects that are already magnetic will react to magnetic fields. 

Therefore, if an iron nail or other object (paper clip, etc) is attracted to a magnet, we must conclude that it feels the magnetic field that surrounds the magnet (otherwise it would not respond at all, like a piece of paper).  This forces us to conclude that the iron nail itself must already be magnetic!  But then why don’t all iron nails attract and repel other iron nails?  In other words, why are some objects able to “become magnetized” when before they exhibited no magnetization? 

The idea that every magnet can be thought of as made up of smaller magnets all pointing in the same direction lends itself to an explanation of how iron, steel, and other metals (nickel, cobalt) can take on magnetic properties in the presence of an already existing magnet.  In an iron nail, for example, we can imagine that before it exhibits magnetic effects, it is as if inside of the iron there are many many tiny magnetic areas, or what we could call magnetic domains (areas inside the iron that are magnetic and have both N and S poles), and that these magnetic domains are all oriented randomly (see picture below).  They can be imagined as acting like little magnets themselves.  Because the magnetic domains are so tiny, and are pointing in all directions, the overall magnetic effect is basically zero – the effects of all the N poles and S poles cancel out overall for distances sufficiently far from the nail.  But if we somehow change the direction in which the magnetic domains point, so that they all line up and point the same way, then the effects of all the little magnetic domains add up and the iron nail becomes a magnet, and can attract paper clips and so on.  We can make the magnetic domains line up by stroking the nail with a magnet so enough of the domains begin to point the same way to make the nail exhibit an overall magnetic effect.  When we do this, we say that magnetism is induced in the iron. 

A section of an iron nail with pictures of the magnetic domains randomly oriented.  No net magnetic field exists at appreciable distances for this magnet so it acts like it had none.

 

 

 

A section of an iron nail with pictures of the magnetic domains after they have all been oriented in the same direction.  The nail now exhibits magnetic effects at appreciable scales, so we call it a magnet!

 

Only certain kinds of materials (we call them magnetic materials) are able to become magnets.  This is because in these materials, iron, cobalt, nickel, some rare or radioactive elements) the magnetic domains are able to move around in response to an external magnetic field.  In things like paper, plastic, cloth, etc, there really aren’t any magnetic domains to speak of, or they are not movable, so they cannot be aligned to produce magnetic effects, nor do they respond to magnetic fields.

Below are pictures on a very very small scale (microns) showing actual measurements of the presence of “magnetic domains” in cobalt (left) and an alloy of yttrium and garnet (right).  The two different areas (dark vs. light) indicate that in some areas a test N pole would be attracted (light lines) or repelled (dark lines).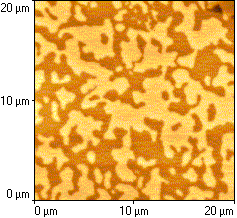

The model of magnetic domains can help to explain:

The model:

 

Home