1.5 The Measurement of Distance

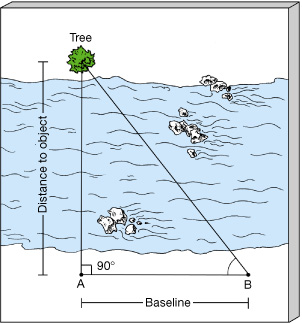
	Figure 1.23 Triangulation Surveyors often use simple geometry and trigonometry to estimate the distance to a faraway object. By measuring the angles at A and B and the length of the baseline, the distance can be calculated without the need for direct measurement.

We have seen a little of how astronomers track and record the positions of the stars on the sky. But knowing the direction to an object is only part of the information needed to locate it in space. Before we can make a systematic study of the heavens, we must find a way of measuring distances, too. One distance-measurement method, called triangulation, is based on the principles of Euclidean geometry and finds widespread application today in both terrestrial and astronomical settings. Surveyors use these age-old geometric ideas to measure indirectly the distance to faraway objects. It forms the foundation of the family of distance-measurement techniques making up the cosmic distance scale.

Imagine trying to measure the distance to a tree on the other side of a river. The most direct method is to lay a tape across the river, but that’s not the simplest way. A smart surveyor would make the measurement by visualizing an imaginary triangle (hence triangulation), sighting the tree on the far side of the river from two positions on the near side, as illustrated in Figure 1.23. The simplest possible triangle is a right triangle, in which one of the angles is exactly 90°, so it is usually convenient to set up one observation position directly opposite the object, as at point A. The surveyor then moves to another observation position at point B, noting the distance covered between points A and B. This distance is called the baseline of the imaginary triangle. Finally, the surveyor, standing at point B, sights toward the tree and notes the angle at point B between this sightline and the baseline. Knowing the value of one side (AB) and two angles (the right angle, at point A and the angle at point B) of the right triangle, the surveyor geometrically constructs the remaining sides and angles and establishes the distance from A to the tree.

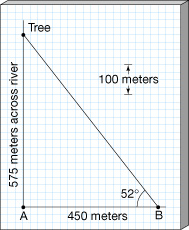
	Figure 1.24 Geometric Scaling We don’t even need trigonometry to estimate distances indirectly. Scaled estimates, like this one on a piece of paper, often suffice.

To use triangulation to measure distances, a surveyor must be familiar with trigonometry, the mathematics of geometrical angles and distances. However, even if we knew no trigonometry at all, we could still solve the problem by graphical means, as shown in Figure 1.24. Suppose that we pace off the baseline AB, measuring it to be 450 meters, and measure the angle between the baseline and the line from B to the tree to be 52°, as illustrated in the figure. We can transfer the problem to paper by letting one box on our graph represent 25 meters on the ground. Drawing the line AB on paper, completing the other two sides of the triangle, at angles of 90° (at A) and 52° (at B), we measure the distance on paper from A to the tree to be 23 boxes—that is, 575 meters. We have solved the real problem by modeling it on paper. The point to remember here is this: Nothing more complex than basic geometry is needed to infer the distance, the size, and even the shape of an object too far away or inaccessible for direct measurement.

Obviously, for a fixed baseline, the triangle becomes longer and narrower as the tree’s distance from A increases. Narrow triangles cause problems because it becomes hard to measure the angles at A and B with sufficient accuracy. The measurements can be made easier by "fattening" the triangle—that is, by lengthening the baseline—but there are limits on how long a baseline we can choose in astronomy. For example, consider an imaginary triangle extending from Earth to a nearby object in space, perhaps a neighboring planet. The triangle is now extremely long and narrow, even for a relatively nearby object (by cosmic standards). Figure 1.25(a) illustrates a case in which the longest baseline possible on Earth—Earth’s diameter, measured from point A to point B—is used. In principle, two observers could sight the planet from opposite sides of Earth, measuring the triangle’s angles at A and B. However, in practice it is easier to measure the third angle of the imaginary triangle. Here’s how.

	Figure 1.25 Parallax (a) This imaginary triangle extends from Earth to a nearby object in space (such as a planet). The group of stars at the top represents a background field of very distant stars. (b) Hypothetical photographs of the same star field showing the nearby object’s apparent displacement, or shift, relative to the distant, undisplaced stars.

The observers sight toward the planet, taking note of its position relative to some distant stars seen on the plane of the sky. The observer at point A sees the planet at apparent location A´relative to those stars, as indicated in Figure 1.25(a). The observer at B sees the planet at point B´. If each observer takes a photograph of the appropriate region of the sky, the planet will appear at slightly different places in the two images. The planet’s photographic image is slightly displaced, or shifted, relative to the field of distant background stars, as shown in Figure 1.25(b). The background stars themselves appear undisplaced because of their much greater distance from the observer. This apparent displacement of a foreground object relative to the background as the observer’s location changes is known as parallax. The size of the shift in Figure 1.25(b), measured as an angle on the celestial sphere, is the third, small angle in Figure 1.25(a).

In astronomical contexts, the parallax is usually very small. For example, the parallax of a point on the Moon, viewed using a baseline equal to Earth’s diameter, is about 2º; the parallax of the planet Venus at closest approach (45 million km), is just 1´.

The closer an object is to the observer, the larger the parallax. Figure 1.26 illustrates how you can see this for yourself. Hold a pencil vertically in front of your nose and concentrate on some far-off object—a distant wall, perhaps. Close one eye, then open it while closing the other. You should see a large shift of the apparent position of the pencil projected onto the distant wall—a large parallax. In this example, one eye corresponds to point A, the other eye to point B, the distance between your eyeballs to the baseline, the pencil to the planet, and the distant wall to a remote field of stars. Now hold the pencil at arm’s length, corresponding to a more distant object (but still not as far away as the even more distant stars). The apparent shift of the pencil will be less. By moving the pencil farther away, we are narrowing the triangle and decreasing the parallax (making accurate measurement more difficult). If you were to paste the pencil to the wall, corresponding to the case where the object of interest is as far away as the background star field, blinking would produce no apparent shift of the pencil at all.

The amount of parallax is thus inversely proportional to an object’s distance. Small parallax implies large distance, and large parallax implies small distance. Knowing the amount of parallax (as an angle) and the length of the baseline, we can easily derive the distance through triangulation. More Precisely 1-4 explores the connection between angular measure and distance in more detail, showing how we can use elementary geometry to determine both the distances and the dimensions of faraway objects.

Surveyors of the land routinely use such simple geometric techniques to map out planet Earth (see Discovery 1-1 for an early example). As surveyors of the sky, astronomers use the same basic principles to chart the universe.

Concept Check

Why is elementary geometry essential for measuring distances in astronomy?